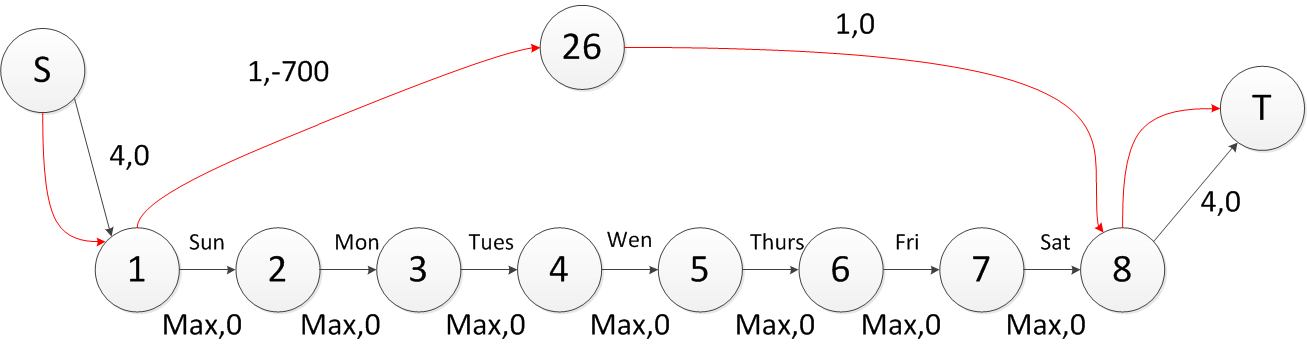
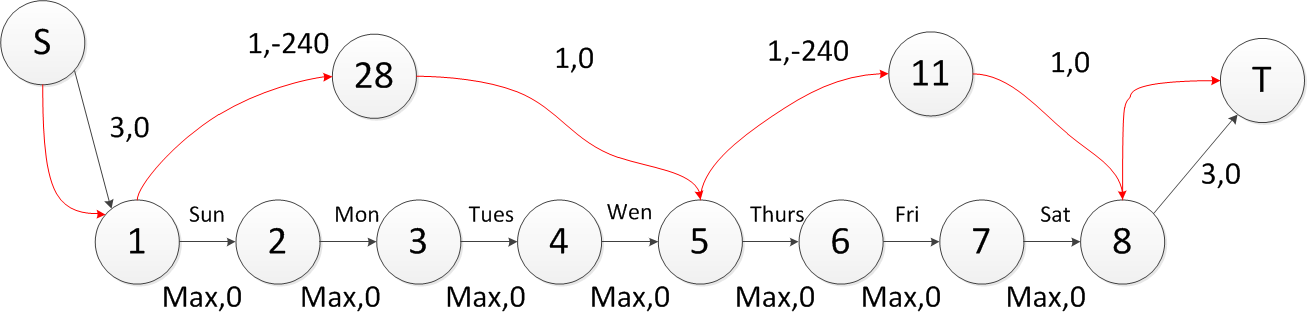
简单多边形的判定
在实际工作中，需要在照片上选定一个范围，这个范围是个多边形，并且是个简单多边形，我们需要判定是否是个合法的简单多边形，主要判定的是任意两边不能交叉。
# 判断两条线段相交
我们可以借助向量的知识来判断两个线段是否相交。二维向量的叉乘(cross product)的几何意义是以两向量为邻边的平行四边形的面积。此外，定义两个向量 a, b。
当 aXb < 0, b 对应的线段，在 a 的顺时针方向。当 aXb = 0时， a 与 b 共线。当 aXb > 0，b 在 a 的逆时针方向。
如果两条线段相交，那必然一条线段的终点和起点，在另外一条线段的两侧。
# 判断多边形两边是否相交
简单并且暴力的方法是检测任意两边是否有交点，在复杂度不高的情况下可以使用这种方法。但是显然是有更优解的，目前比较有名的两个算法是 The Bentley-Ottmann Algorithm 和
The Shamos-Hoey Algorithm。算法的细节请查看下方的参考，我就不详细描述了。
# 简单多边形判定的实现
export interface Point {
x: number;
y: number;
}
export interface Line {
start: Point;
end: Point;
}
function samePoint(p1: Point, p2: Point) {
if (p1.x === p2.x && p1.y === p2.y) {
return true;
} else {
return false;
}
}
function signedArea(p1: Point, p2: Point, p3: Point) {
return (p1.x - p3.x) * (p2.y - p3.y) > (p2.x - p3.x) * (p1.y - p3.y);
}
function intersectLine(l1: Line, l2: Line) {
// consecutive edge return false
if (
samePoint(l1.start, l2.start) ||
samePoint(l1.start, l2.end) ||
samePoint(l1.end, l2.start) ||
samePoint(l1.end, l2.end)
) {
return false;
}
return (
signedArea(l1.start, l2.start, l2.end) !==
signedArea(l1.end, l2.start, l2.end) &&
signedArea(l1.start, l1.end, l2.start) !==
signedArea(l1.start, l1.end, l2.end)
);
}
export function intersectPolygon(points: Array<Point>) {
const len = points.length;
for (let i = 0; i < len - 1; i++) {
for (let j = i + 1; j < len; j++) {
const l1: Line = {
start: points[i],
end: points[(i + 1) % len]
};
const l2: Line = {
start: points[j],
end: points[(j + 1) % len]
};
if (intersectLine(l1, l2)) {
return true;
}
}
}
return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
# 总结
简单多边形判定的本质是任意两边是否相交，如果是邻边的话就直接跳过。在复杂度不高的情况下，可以直接使用遍历的方法来实现。
# 参考
Intersections of a Set of Segments (opens new window)
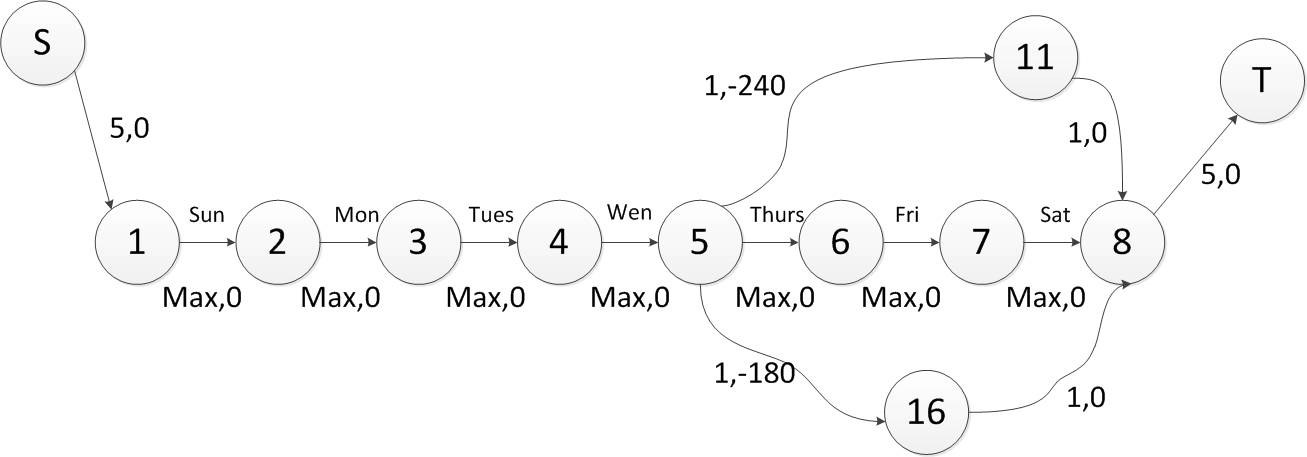顶点 11 和顶点 16 是重复边的订单,对应的是第一个订单和第 6 个订单.源码和输入数据可以在文章末尾看到.
